Normal

Self-replicating or self-copying programs are kind of interesting to play with. They are also called Quine. Here is one written in C, by Vlad Taeerov and Rashit Fakhreyev.

main(a)

{

    printf(a,34,a="main(a){printf(a,34,a=%c%s%c,34);}",34);

}

I adjusted it to work on Code::Blocks:

#include <stdio.h>

main(char*a)

{

  printf(

    a,

    34,

    a="#include <stdio.h>\nmain(char*a){printf(a,34,a=%c%s%c,34);}",

    34);

}

This a prolog version I created:

q :-

        listing(q),

        write(':-q.').

:-q.

It could have been shorter, but you would have to query ‘q’. This is it:

q:-listing(q).

This is a simple application of function pointers. Here I am trying to sort an array points based on X values, Y values or the distance from the origin. I have a simple sorting algorithm and the sorting criteria can be changed by using function pointers. 

Lets start with the types we need. First, I need a structure to hold the X and Y values of the point. Point2D structure takes care of that. Second, a type that will define the sorting criteria, see in line 9. It define a pointer to a function that accepts two arguments both of which are Point2D structures and returns a bool. Typically comparison operations have this format.

   1:  #include <iostream>

   2:  #include <math.h>

   3:  using namespace std;

   4:   

   5:  // 2D co-ordinate system

   6:  typedef struct _Point2D

   7:  {    double X, Y;}Point2D;

   8:  // function pointer type definiton

   9:  typedef bool (*Compare)(Point2D&,Point2D&);

Lets define a function to create and initialize a Point2D structure. This will make it easier to control or set default values to the Point2D structure.

  10:  // function that returns a 2D point

  11:  Point2D fnCreatePoint(const double x=0.0,const double y=0.0)

  12:  {

  13:      Point2D point;

  14:      point.X = x;

  15:      point.Y = y;

  16:      return point;

  17:  }

Lets further define swap function usually used in sorting algorithms and a simple sorting function. There are fairly direct, if you need more help with this see: Swap, Bubble Sort. Note that the sorting algorithm takes a additional argument of type Compare. That is the type of the function pointer that will define the comparison criteria while sorting.

  18:  // swaps the two values

  19:  void swap(Point2D& a,Point2D& b)

  20:  {

  21:      Point2D t;

  22:      t.X = a.X;t.Y = a.Y;

  23:      a.X = b.X;a.Y = b.Y;

  24:      b.X = t.X;b.Y = t.Y;

  25:  }

  26:  // sorts an array of values

  27:  Point2D* sort(Point2D* points,const int len,Compare fnCompare)

  28:  {

  29:      for(int i = 0;i<len;i++)

  30:          for(int j = i+1;j<len;j++)

  31:              if(!fnCompare(points[i],points[j]))

  32:                  swap(points[i],points[j]);

  33:      return points;

  34:  }

Now, that we have the framework we need, let us define a few comparing functions. These are simple functions that perform a particular type com comparison. The compare_x function compares only the X value of the Point2D structure. Similarly, compare_y function compares the Y value. The compare_distance function calculates the distance from the origin for the two points and then compares the distance. Note that each of these functions follow the argument types and return value type defined previously in line 9. 

  35:  // comparing functions

  36:  bool compare_x(Point2D& a,Point2D& b)

  37:  {     return a.X < b.X;}

  38:  bool compare_y(Point2D& a,Point2D& b)

  39:  {     return a.Y < b.Y;}

  40:  bool compare_distance(Point2D& a,Point2D& b)

  41:  {     return

  42:          sqrt(pow(a.X,2.0) + pow(a.Y,2.0)) <

  43:          sqrt(pow(b.X,2.0) + pow(b.Y,2.0));

  44:  }

We have all the components that are needed to make this work. Here, I create an array with five points in it and call the sorting algorithm with the appropriate comparison criteria. Finally, display the sorted array of points.

int main()

{

    Point2D points[]={

        fnCreatePoint(-1,1),

        fnCreatePoint(-2,2),

        fnCreatePoint(1,-1),

        fnCreatePoint(2,-2),

        fnCreatePoint(0,0)};

    int length = 5;

    cout << "Sorted by X value:" << endl;

    // Sorts the points based on X

    sort(points,length,compare_x);

    Display(points,length);

    cout << endl << "Sorted by Y value:" << endl;

    // Sorts the points based on Y

    sort(points,length,compare_y);

    Display(points,length);

    cout << endl << "Sorted by distance from the origin:" << endl;

    // Sorts the points based on distance from the origin

    sort(points,length,compare_distance);

    Display(points,length);

    return 0;

}

I hope this helps you understand function pointers. Source code: fptr_example.cpp

I have often seen that there is a confusion around the ‘void’ concept in C++ among the new comers to C++. Especially when it is used as a pointer. A commonly seen definition is that void means lack of something. Hence you cannot have a variable of type void. But you can have a pointer which is of void type. This is a bit confusing, so I am going to try and give examples and explain about each one.

Before I start, a pointer stores the address to some content. So, the size of all pointers are the same regardless of the content they point to. However, the pointer arithmetic depends on the type of content it is pointing to. Here I am going to talk about a type that means nothing and can be used to point to any type.

1. void vX;

This is NOT allowed in C++. You cannot have a variable of type void. This makes some sense, void means nothing, hence you cannot declare a variable of type nothing. A variable is a name for a location in memory, and since void does not define the amount of memory needed you cannot allocate it.

2. void fnDoSomething(void);

This is allowed in C++. This says that the function fnDoSomething accepts nothing and returns nothing. There is no memory  needed to store the variables here. However, void fnDoSomething(int iX, void); is invalid. This is trying to say fnDoSomething accepts an integer and the next argument is nothing. The compiler will show an error indicating that the type of the second argument is not known or invalid use of void. Since we are passing values the compiler has to put code in there to copy the value that will go into ‘iX’, so before copying memory has to be allocated for that argument. The first argument is fine because the compiler knows the cost of int and it can allocate the amount of memory needed for it. When the compiler looks at the second argument, it cannot allocate memory because of the problem we saw in section 1. Finally, void fnDoSomething(); has the same meaning as void fnDoSomething(void); . Here is a simple example:

   1:  void fnSomething(void)

   2:  {

   3:      cout << "Something was done.";

   4:  }

3. void *vpX;

This is allowed in C++. First, a pointer is being declared. This is allowed but NOT ‘void vX;’ because here a pointer was created and we are telling the compiler not to care about the type of the item it is pointing to. Usually, the amount of memory for any type of pointer is 4 bytes (8 bytes for x64). Second, since it is a pointer the compiler knows the amount of memory it needs to allocate, and ‘vpX’ is the name for that allocated memory.  A void pointer can point to any variable (except for those which are const or volatile) or can point to a function (except for member functions of a class).  Here is an example, the program  prints the byte sequence from memory for int and double data types using the same function.

   1:  void fnPrintHex(void *vpData,int iSize)

   2:  {

   3:      unsigned char* cpData = (unsigned char*)vpData;

   4:      for(int i=iSize-1;i>=0;i--)

   5:          cout << hex << (int)*(cpData+i);

   6:  }

   7:   

   8:  int main()

   9:  {

  10:      int iX =1234;

  11:      fnPrintHex(&iX,sizeof(iX));

  12:      cout << endl;

  13:   

  14:      double dX = 1234.5678;

  15:      fnPrintHex(&dX,sizeof(dX));

  16:      cout << endl;

  17:   

  18:      return 0;

  19:  }

4. const void *vpX;

This is allowed in C++. This means that the void pointer points to a constant value. The following will cause a type-cast error during compilation:

   1:  const int iX = 10;

   2:  void *vpX = &iX; // Type cast error

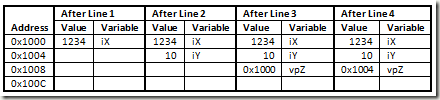
Only a const void type pointer is allowed to point to a constant. This means that the pointer itself is NOT constant and its value can be changed. But, the value it is pointing to is supposed to be constant. Note, const T *pX = &X is valid, T here is the same type as X. In the following code, in line 3 the ‘vpZ’ pointer is assigned the address of ‘iX’ and in line 4 it is reassigned with address of ‘iY’. The following code should print 1234 and 10, on separate lines.

   1:  const int iX = 1234;

   2:  const int iY = 10;

   3:  const void *vpZ = &iX;

   4:  vpZ = &iY;

   5:  cout << iX << endl << *(const int*)vpZ;

There is a minor issue here. Note that in the above code both ‘iX’ and ‘iY’ are constants and their value cannot be changed. But, you’ll see that you can do something as shown in the code below. If you read the code it may seem like it’ll print 1000 and 1000 on separate lines. Well it actually prints 1234 and 1000 on separate lines. Constants are optimized, hence the value of ‘iX’ gets placed wherever it is used. But, the original memory location is still alterable since it was type-cast to a editable type. Note, some debuggers will show the value of ‘iX’ on line 4 as 1000, you may have to test this on your compiler and debugger.

   1:  const int iX = 1234;

   2:  const void * vpZ = &iX;

   3:  *(int*)vpZ = 1000;

   4:  cout << iX << endl << *(int*)vpZ;

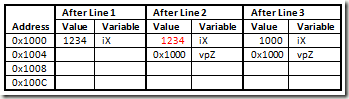
In the figure above, the number is highlighted in red because the compiler would have already picked up the value and applied everywhere ‘iX’ is used. So even if the value is changed it no longer matters wherever ‘iX’ used.

5. void *const vpX;

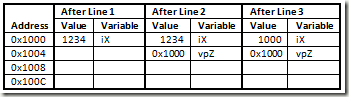
This is allowed in C++. This means that the void pointer itself is a constant but it points to a variable. So, once an address is assigned to the pointer, you cannot reassign another address to it. In line 3 an address is assigned to ‘vpZ’ and after that line ‘vpZ’ cannot be assigned another address.

   1:  int iX = 1234;

   2:  int iY = 10;

   3:  void *const vpZ = &iX;

   4:  vpZ = &iY; // This is NOT allowed

But, the content at the address where the void pointer points to can be changed. You need to type-cast before you can make any changes. See the following code, it prints out 1000 and 1000, on separate lines.

   1:  int iX = 1234;

   2:  void *const vpZ = &iX;

   3:  *(int*)vpZ = 1000;

   4:  cout << iX << endl << *(int*)vpZ;

6. const void* const vpX;

This is allowed in C++. This is a void pointer which is a constant pointing to an address whose contents are also constant. This is a combination of section 4 and 5 and the same rules apply. The following code will fail to compile, see section 5 for the reason:

   1:  const int iX = 1234;

   2:  const int iY = 5432;

   3:  const void *const vpZ = &iX;

   4:  vpZ = &iY; // This is NOT allowed

But the following code is allowed, see section 4 for the reason:

   1:  const int iX = 1234;

   2:  const void *const vpZ = &iX;

   3:  *(int*)vpZ = 1000;

   4:  cout << iX << endl << *(int*)vpZ;

I tested all of my code in visual C++ and GNU GCC. Please let me know if there are any mistakes. This is an introduction, I’ll try and write more advanced usage of void pointers in the future. Thanks for your patience.

This is a simple Sudoku solver in Prolog. I was experimenting with Prolog and its backtracking mechanism. In the code, there is a ‘start’ predicate which can be called to run the code and test it out. It is fairly easy to modify and adapt to other problems of this kind. This was written and tested on SWI-Prolog (download here). Source for the Sudoku Solver: sudoku

In “Errors as we speak”, we saw how error prone communicating with words can be. Let’s explore a deeper level of translation between idiolects, and how our mind achieves this translation.

Psychology has taught us that we communicate people with a mental “looking glass”, which filters content based on the idiosyncrasies of the individuals it has picked up. We have a general looking glass that we use to communicate with strangers. This general looking glass is conditioned by every experience accumulated till date. It allows us to make choices such as mode of speech, body language, subtleties in the intonation of words, etc. This general looking glass works until the conversation remains general (definition of ‘general’ is relative to each individual).

As we learn more about a person, we seize to use the general looking glass and we switch to a specialized one, dedicated to the person. This can be observed in our daily life and we understand some people who are close to us, even if they were not able create a complete sentence about whatever they were trying to say. This is because, the looking glass, with time, has now tuned to pickup and translate, a person’s idiolect to one’s own idiolect. In essence, our mind captures the personality of the individuals. One might ask, why do we need this mechanism? What purpose does capturing one’s personality have?

Our mind is a sucker for running simulations. Call it imagination, prediction or contemplating outcome, it is an important feature which allows us to form social groups. Capturing personalities allows our mind to estimate the consequences of our actions by predicting reactions of people. By using the feedback from the predicted reactions our mind to improve its strategy, prepare itself for consequences.

This ability of our mind is so good that it can associate personality to everything, be it an animate (pet animals) or inanimate (bike, tools), existing (anything tangible) or imagined (characters in a book) objects. It so well evolved that sometimes we can communicate using the looking glass, within our mind, and yet come up with a response which exactly reflects the response of the person we just simulated, this almost sounds like telepathy. Although our mind has evolved this feature, we don’t have complete control over it.

It is all about exchange of ideas. In this world of information exchange, we designed transmission mechanisms that are, in effect, error free. But, we have forgotten the most fundamental of transmission mechanisms that isn’t yet perfect. It took nature millions of years of evolution to perfect some of its technologies, and communication mechanism of humans, i.e., speech, isn’t one of them.

The Source: Information exchange, in any form, has two terminal components a Source and a Destination. Let’s, begin with the source. We are yet to figure out how information content is stored and operated on in the brain. But we sure don’t think with words, although, words do contribute, in part, in guiding the thought process. The problem appears when it is time to transfer the idea from our mind to any form of media tangible or intangible. One form of presenting our idea is with words and this is where conversion from abstract idea to words has to happen.

The Encoder: We convert an idea to words by selecting those which, to us, at that moment, are our best approximation to the abstractness of the idea. My friend, Tom Horton, calls it “bag of words”. We pick words, depending on the vocabulary and our meaning for that (based on visceral feeling we have for the word). Since our choice is an approximation, finally, our presented idea, after conversion, is an accumulation of approximation.

The Medium: Words can be transferred using a myriad of media, but I want to look at the medium we were born with. I believe that it is easily subjected to errors compared to other forms. Firstly, words have to be converted to sound, this happens by picking up a sequence of pulses which control the vocal chords. These sequences of pulses were learnt, which means another layer of approximation is introduced.  Then we expect the vocal chords to reproduce the sound and we have introduced another layer of errors. Secondly, the generated sound travels through the air (assumed to be speaking with someone in person), superimposed by noise, introducing a major layer of error. Lastly, the transfer is incomplete without reception. Ears pick up this sound, slightly obfuscated, and compares and picks up the words that have the highest probability of correctness, based on physical comparison of sounds, context and several hundreds of other fact0rs, etc.

The Decoder: Let’s face it; this is a real tough one. It is difficult to find someone who has at least one neuron that can fire, let alone find someone and get them to completely understand something by explaining it to them. As with the encoder, the words after being captured have to be transformed into the idea, or the abstract form. Since each person has a different visceral feel for words the transformation is never prefect.

The Destination: I believe that the destination for a transferred idea is reached when the intended person begins to understand the concept. However, each person thinks with physics of his own. The rules that govern the through process in each individual person is different, which brings us to a conclusion that each person understands the world differently. I conclude my rant here, that have patience when explaining things to others.

Disclaimer: I have not added any references to the claims I have made here because it is a rant. If you did learn anything from it, I beg your pardon, it was purely accidental.

Anyone who has worked with Machine Learning would have used the Logistic Regression algorithm, or at least heard about it. Well, here is a simple application that observes you play, and learns, how to play the game of Tic-Tac-Toe.

How does it work?

As you play the game the algorithm observes the game. It isolates the choices that you made which led you to win the game. The draw and losing cases are not used. It then uses Logistic Regression to train the underlying intelligence, let us represent it by “”. As it gains more experience, it’ll be able to make more accurate predictions about the game and hence it learns to play the game.

The math behind it

It uses Gradient Descent along with Logistic Sigmoid function to train and predict. Prediction in this application is done by nine individual Logistic Regression units, and the outcome of each of them corresponds to one of the nine possible spaces  in the Tic-Tac-Toe game.

Let be the indexes of nine spaces in the game. Also let, represent the space chosen by you (to mark either X or O). Let, represent the input to the algorithm (see Figure 1). The intelligence that maps the input to a predicted output be represented by . The prediction for the space is made as per the equations shown below:

Note: is the bias parameter. It has the same effect as applying Affine Transform to the polynomial.

Here, represents the predicted output and represents the move made by you. So, the purpose of training process is to adjust the values of until . This is done using the Gradient Descent algorithm.

	Learning Rate, a real valued number that indicates how fast the training algorithm converges.
	Number of training samples.
	Intelligence parameter indicating how the input affects the output.
	Actual output for the space given sample as input.
	Predicted output for the space given sample as input.
	Represents the input sample.
	Represents the value of the space in the input sample.

How does all that work?

Below is a Silverlight version of the application, try it out. After you play the first game, you should see some prediction. The darkest circle is where the prediction algorithm thinks that you will make the next move. Here is the link to the source code: TicTacToe.zip. Note, you have to move for both the players. The predictor only predicts the moves. Until you play the first game with a winning outcome the predictor will not be trained.

To put it simply,

Replace by any of the functions from the following table, it also shows the effect of the function on the “Lenna” image. The images show effect of morphology or filter applied in the frequency domain.

Source Code: C++

f(x)	Processed Image
Dilate(x) : Morphological Dilate
Erode(x) : Morphological Erode
Open(x) : Morphological Open
Close(x) : Morphological Close
Gradient(x) : Morphological Gradient
Gaussian(x) : Simple Gaussian Blur

Images processed with FFTW and OpenCV libraries.

1. Hyperbolic Discounting:

We are evolutionarily designed not to think of the future, hence our brain sucks at making evaluations when similar rewards are presented with a time difference. We tend to choose the one that arrives sooner than later. For instance, when offered the choice between $50 now and $100 a year from now, many people will choose the immediate $50. However, given the choice between $50 in five years or $100 in six years almost everyone will choose $100 in six years, even though that is the same choice seen at five years’ greater distance.
Ref: Hyperbolic Discounting

2. Understanding Sunk Cost:

Again another evolutionary feature that makes us believe that we need to make our invested resources count even after we know that it was a clear waste. For instance, let’s say you’re in the market for a replacement computer, and the best thing for what you want is a $500 PC. However, you’ve always been a Mac user and recently bought $600 on a wireless Apple keyboard. Now, even though you like everything better about the Dell (it comes with its own wireless keyboard), and it’s twice as cheap as the nearest Mac equivalent, your brain will tell you not to waste the money you spent on the keyboard. So, in the name of not letting the keyboard go to waste, you buy the Mac.
Ref: Sunk Cost
Example: source Cracked.com

3. The Disposition Effect:

In simple terms, instead of acknowledging losses in an investment, such as stocks which will never go up in value in reality, we instead wait for the value to go up. Although, the proper plan would be to sell and salvage, whatever possible, before the value drops further. This also includes storing stuff that you don’t need thinking that you’ll need it after you dispose it.
Ref: Disposition Effect

4. Irrational Escalation of Commitment:

This one stems from our ability to convince ourselves that we are right in our wrong decisions. This is seen in competitive scenarios, such as bidding, where one might end up paying more than the actual worth of an object quite simply to justify the competitive instinct.
Ref: Irrational Escalation of Commitment, Dollar Auction

5. Post-Purchase Rationalization:

Here we try to convince ourselves that the resource we just spent on nothing was actually worth it. This is not just money, can be anything, like time. This behavior of ours makes us believe that the procrastinated time was worth it. In terms of investment, you will keep investing in something just because you already invested in it. For instance, when faced with the prospect of a $3,000 repair on your car, or purchasing a slightly cheaper model car for $2,500, your brain will tell you to go with the repairs because you already sunk $10,000 on it. Your brain will have convinced itself that the last decision was a great idea. And since you’ve now sunk $13,000 into the car, it’s going to seem like an even better idea to keep piling up the bad decisions. On a similar note, be sure to read about the IPhone syndrome.
Ref: Post-Purchase Rationalization
Example: source Cracked.com

6. Money Illusion:

According to our brain $10 bill not equal in worth as ten $1 bills. Also, you are more likely to squander the money if you have ten $1 bills as compared to one $10 bill.
Ref: Money Illusion

7. Gambler’s Fallacy:

Our brain is terrible at probability, and the entire lottery business is based on this fact. For instance, if you flip a coin repeatedly and you get heads more than usual, then you are likely to think that you are going to get tails more often in the future or if you are not among the common then you may bet on heads. But, in reality, the odds of getting a head or tail is always same, for a fair coin.
Ref: Gambler’s Fallacy, Why Poor People Win The Lottery

I was trying to work with passing data between multiple Silverlight components and Windows.Messaging provides the support just to do this. It is as simple as creating instances of LocalMessagingSender and LocalMessagingReceiver and calling a function to send.

In the example below, the mouse position upon MouseMove is sent as a message. Note: I have used fixed global naming for the receiver so if you open multiple copies of this blog ( in other browsers or in the same browser ) you may get an exception, but you can open any number of sender pages.

This is the sender ( click here to open sender in a new page ):

This is the receiver :

Project files: LocalMessaging.zip