Normal

I was working on a project to find out the optimal network structure for a multi-layered perceptron, and I found that this technique could be very useful. All though, in this example I am keeping the concept simple, the network structure that I have used here is a fixed one, but the best network is selected using Genetic Algorithm. In this example I have created a artificial world where the creatures can survive to the next generation if they learn faster.

I have created a simple environment for the digital creatures where they can only survive if they can perform binary addition.  The purpose of this experiment was to create an environment where these digital creatures evolve and learn binary addition in the process. I am forcing them to learn binary addition, for quicker results.

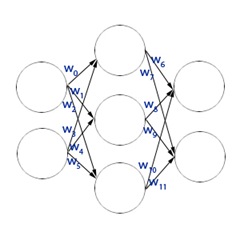
Each digital creature is composed of 7 neurons, in a 2:3:2 layout. The network of neurons is of fully connected type. The DNA sequence of these creatures defines the connection strength between the various neurons. The first generation of digital creatures has connection weights selected by using random values. With each stage they provide the basic information required to survive with the environment to the next generation.

Each generation gains some experience by living within the environment for certain number of cycles. During this stage they are trained using the Back-Propagation algorithm. They are trained for only a certain number of cycles after which the elites in the population are chosen. Elites are those which have the best chance of survival, and are selected as members of the next generation. The remaining members for the next generation are created by paring the members of the current population.

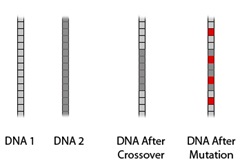
The difference between the elite members and other members is that elite members have their DNA intact, where as other members will have modified versions of the DNA. The DNA is modified by a process called Crossover, where the paired members contribute a part of their DNA to the next generation. This new DNA may sometimes be further modified by another phenomenon – Mutation. In Mutation a randomly selected gene gets replaced by a new gene. Both, Crossover and Mutation may have either positive or negative effects on the creature which will be formed using the modified DNA.

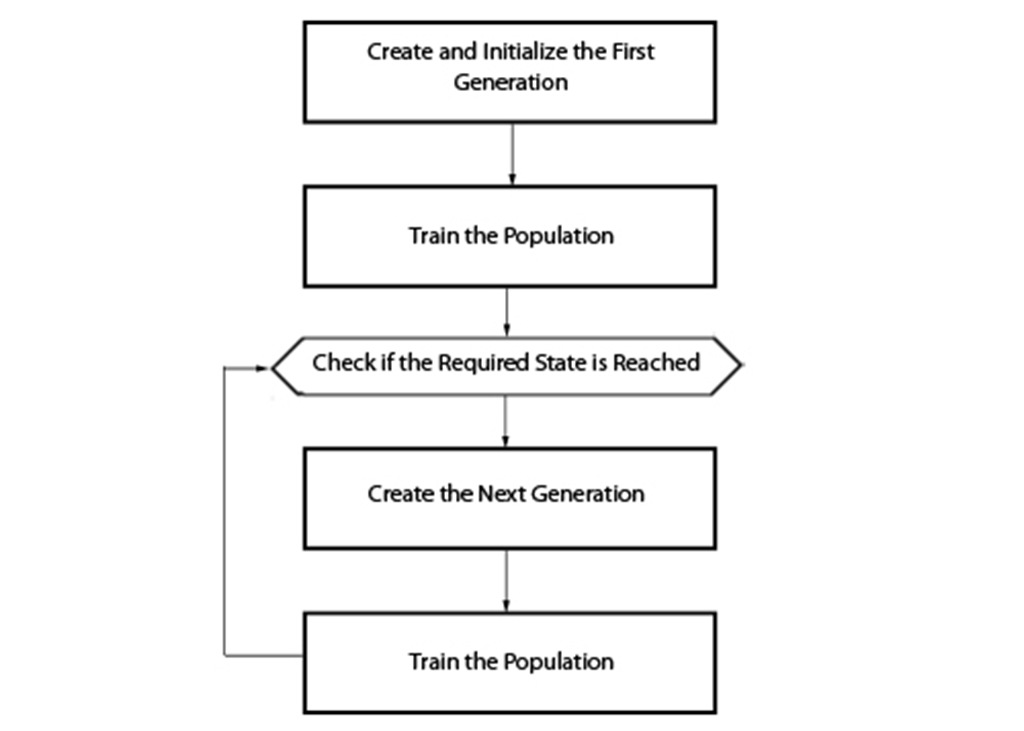
The Algorithm:

The first step is to create a base population and allow it to train. Then check if the required state is reached, if not, then  move to next generation. Train the new generation and again check if the required state is reached. Repeat until the optimum solution is obtained. Flow diagram for the algorithm is shown below:

1. Creating the First Generation: This step involves creating the Neural Network for each of the member for the first generation. The network is initialized with weights generated using Nguyen-Widrow algorithm. The input and output values are scaled so that they are normalized.
2. Training: Each member of the population is run through a predefined number of training cycles. The ANNs are trained using the Back-Propagation Algorithm. The version of back-propagation algorithm used in the example has been slightly modified, so that the convergence is faster. Also, the training samples are shuffled before each training cycle.
3.  Required State: To test the required state, a sample input is given and the output which is received will be compared with expected output. If the difference is lower than a predefined error threshold then the required state is reached and the process will be stopped. Otherwise, the process will be repeated until it is reached.
4. Creating the Next Generation: To create the new generation we need to select the elites first and then we can create more members by randomly paring the members of the current population. Elites are those members who have the least error when a sample input is provided. The number of elites in a population is selected based on a ratio which will be around 10% to 30% of the total population. The remaining members for new generation are created by crossover paring. Here, certain traits from each of the member in a pair are selected and a new DNA is formed. This new DNA will be used to create a member for the next generation. During crossover Mutation can occur and occurrence of this is determined by a probability factor.

The Digital Creature:

As I had mentioned earlier, each digital creature has 7 neurons arranged in 3 layers. The neuron connection diagram is shown below (each of the circles represent a neuron). That’s all there is to it, each creature is a simple fully connected Multi-Layer Perceptrons(MLP).

The DNA:

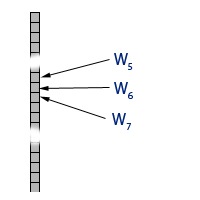
For this project I have used a mapped DNA, i.e., each of the weights that are marked in the neuron structure diagram are directly map to a gene on the DNA. The figure below will give you a better idea.

Crossover and Mutation:

Consider two DNA strands, let’s call them DNA1 and DNA2. With the crossover process we’ll end up with a new DNA that has some genes for DNA1 and some from DNA2. Since in this project I have directly mapped neuron connection weights to genes, the new DNA contains connection weights of the contributing DNA strands. As for the mutation part, it’s just a random value, but the value is selected to be within the range of the original DNA strand.

Advanced form of the example:

In an advanced form of this example, instead of the direct mapping of the genes to the neuron connection weights, there would be a more complex DNA which had control over number of layers and number of neurons per layer also the type of transfer function for each layer of neurons and finally the weights. To make in more interesting instead of forcing them to learn binary addition, they would be allowed to develop it by reward strategy. Though this is interesting, the time it takes for them to develop binary math will be too long. So, for now this example should be enough to demonstrate the possibility.

Working with the project files:

The project was built using Visual Studio 2008. Just extract the contents of the ZIP file and run the project. The default values are preset, so just press "Run". The result will be displayed on the right side, which will show the number of generations it took to reach the prescribed error threshold, current error and also the result of binary addition using the elite member of the latest generation.

If only "Android 18" was so easy to build.